Code
# specify prior and data generation mechanism
## hyperparameters
alpha = 1
beta = 1 ### thus an uninformative prior
##
theta = 0.45
n = 100
set.seed(0808)
y = rbinom(n, 1, prob = theta)Under the Bayesian paradigm, the statistical inference is conducted on the posterior distribution of parameters or the posterior predictive distribution of outcomes depending on the quantity of interest. In most cases, the posterior distributions are complex and known up to a constant factor (unknown) at best. It is Markov Chain Monte Carlo (MCMC) that makes the posterior estimation/inference doable and easier via simulating draws from the posterior distribution.
Today, how MCMC works is not the focus. Instead, I will use several examples to illustrate conducting Bayesian inference with Stan (based on Hamiltonian MCMC) in R.
First of all, we should install rstan package, the R interface to Stan, and the tools for compilation of C++ code in our computer. (Refer to Stan official guide for details.)
Example 1, beta-binomial
\[ \theta \sim \text{Beta}(\alpha,\beta) \]
\[ Y|\theta \sim \text{Bernoulli}(\theta) \] Observed data, \(\{y_1,y_2,...,y_n\}\) (iid).
\[ p(\theta|\boldsymbol{y})\propto p(\boldsymbol{y}|\theta)\pi(\theta)\propto \theta^{\sum_i y_i}(1-\theta)^{n-\sum_i y_i}\theta^{\alpha-1}(1-\theta)^{\beta-1} \]
Therefore,
\[ \theta|\boldsymbol{y}\sim \text{Beta}(\alpha+\sum_i y_i,\beta+n-\sum_i y_i) \]
This posterior distribution is a well-known distribution and we don’t bother to use Stan; it is chosen mainly to have theoretical results to compare with those obtained from Stan.
Before we call Stan in R, we need to create a .stan file (easy to do in Rstudio) written in Stan language, pretty straightforward and concise. (Stan Reference Manual for language details)
Code
data { // Y is the observation vector with N observations
int<lower=0> N;
array[N] int Y;
}
parameters { // theta is bounded between 0 and 1
real<lower=0, upper=1> theta;
}
model {
theta ~ beta(1, 1); // specify prior distribution
for(n in 1:N){
Y[n] ~ binomial(1, theta); // specify model for data
}
}Now we can load rstan package and call stan function to simulate a posterior sample. (For this example, executable Stan code is inserted to output a stanmodel for sampling function as input. If we create a separate .stan file in the same directory, use stan function.)
Code
library(rstan)
options(mc.cores = parallel::detectCores()) # parallel computing, one chain per core
rstan_options(auto_write = TRUE) # only need one time of compilation of C++ code
dat = list(N=n, Y=y) # consistent with data block in .stan file
beta_binomial_fit = sampling(beta_binomial_model, data = dat, algorithm="HMC")Initial points (values) for MCMC are likely to influence the time it takes for the chains to reach the stationary distribution (target posterior distribution). Thus, draws during sampling period (default, 1001-2000) of each chain (default, 4 chains) are collapsed together to form a final posterior sample.
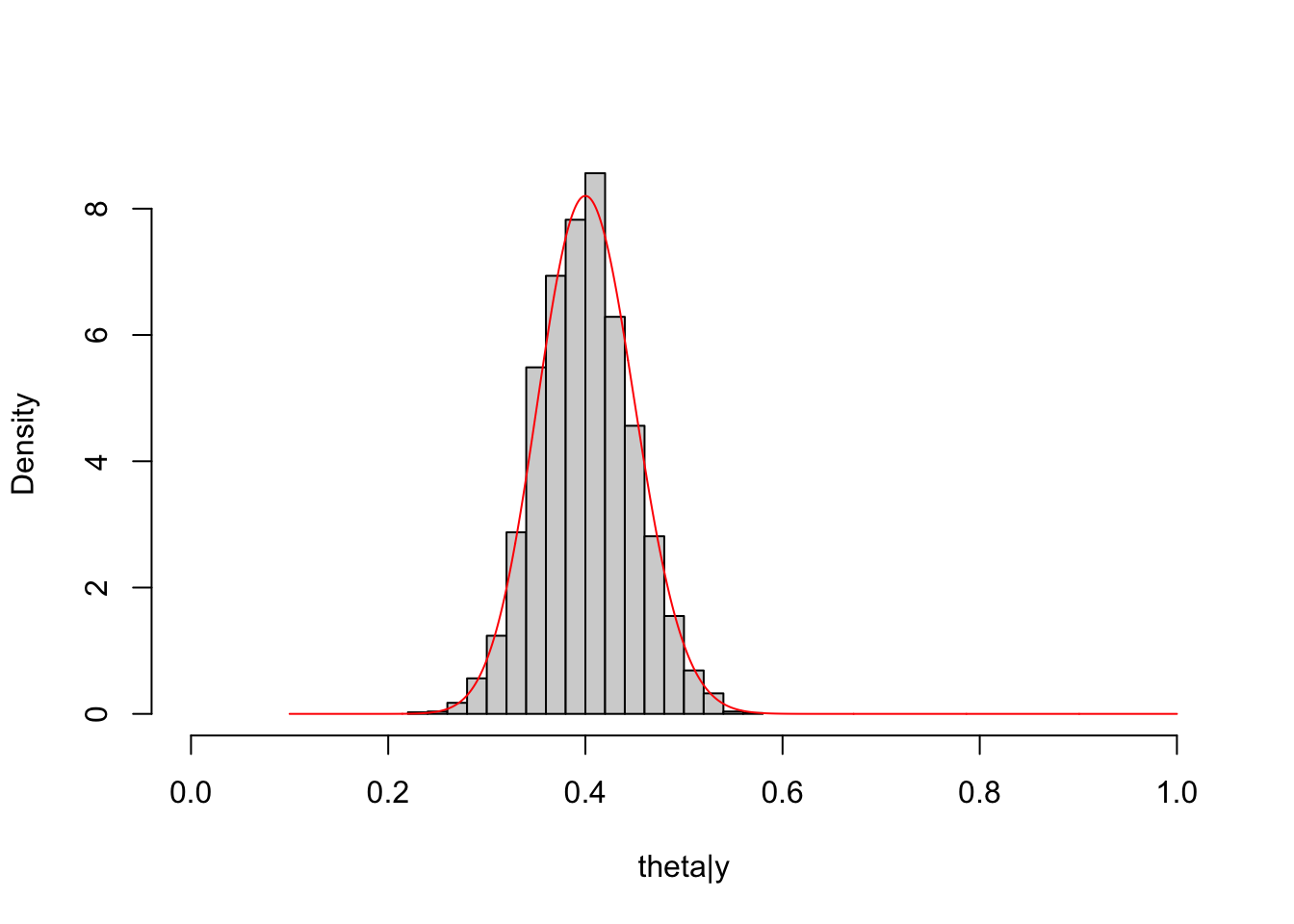
The match between the histogram of the sample and the theoretical density curve of the posterior distribution is satisfactory.
Code
theta_post = extract(beta_binomial_fit, permuted=T)$theta
hist(theta_post, freq = F, main = NULL, xlim = c(0,1),
xlab = "theta|y")
lines(seq(0.1, 1, length.out = 1000), dbeta(seq(0.1, 1, length.out = 1000),
shape1 = alpha+sum(y),
shape2 = beta+n-sum(y)),
col="red")
Example 2, normal-normal
\[ \mu\sim N(\mu_0, \sigma_0^2) \]
\[ Y|\mu,\sigma^2\sim N(\mu, \sigma^2) \]
\[ p(\mu|\boldsymbol y)\propto \exp(-\frac{(\mu-\mu_0)^2}{2\cdot \sigma_0^2})\exp(-\frac{\sum_i (y_i-\mu)^2}{2\cdot \sigma^2}) \]
Therefore,
\[ \mu|\boldsymbol {y}\sim N(\frac{\frac{1}{\sigma_0^2}\mu_0+\frac{n}{\sigma^2}\bar y}{\frac{1}{\sigma_0^2}+\frac{n}{\sigma^2}},\frac{\sigma_0^2\sigma^2}{n\sigma_0^2+\sigma^2}) \]
Code
# set prior and generate data
mu_0 = 0
sigma_0 = 1
mu = 1.5
set.seed(0808)
y_normal = rnorm(n, mean = mu, sd = 5)
dat_normal = list(N=n, Y=y_normal)(Refer to this for functions defined in Stan)
Code
data { // Y is the observation vector with N observations
int<lower=0> N;
array[N] real Y;
}
parameters { // mu is unbounded
real mu;
}
model {
target += normal_lpdf(mu|0, 1);
target += normal_lpdf(Y|mu, 5);
}Code
# MCMC and plot
normal_normal_fit = sampling(normal_normal_model, data = dat_normal, iter=2000, chains=4)
mu_post = extract(normal_normal_fit, permuted=T)$mu
hist(mu_post, freq = F, main = NULL,
xlab = "mu|y", xlim=c(-1,4))
lines(seq(-1, 4, length.out = 1000), dnorm(seq(-1, 4, length.out = 1000),
mean = (mu_0/sigma_0^2+sum(y_normal)/5^2)/(n/5^2+1/sigma_0^2),
sd = sqrt(5^2*sigma_0^2/(n*sigma_0^2+5^2))),
col="red")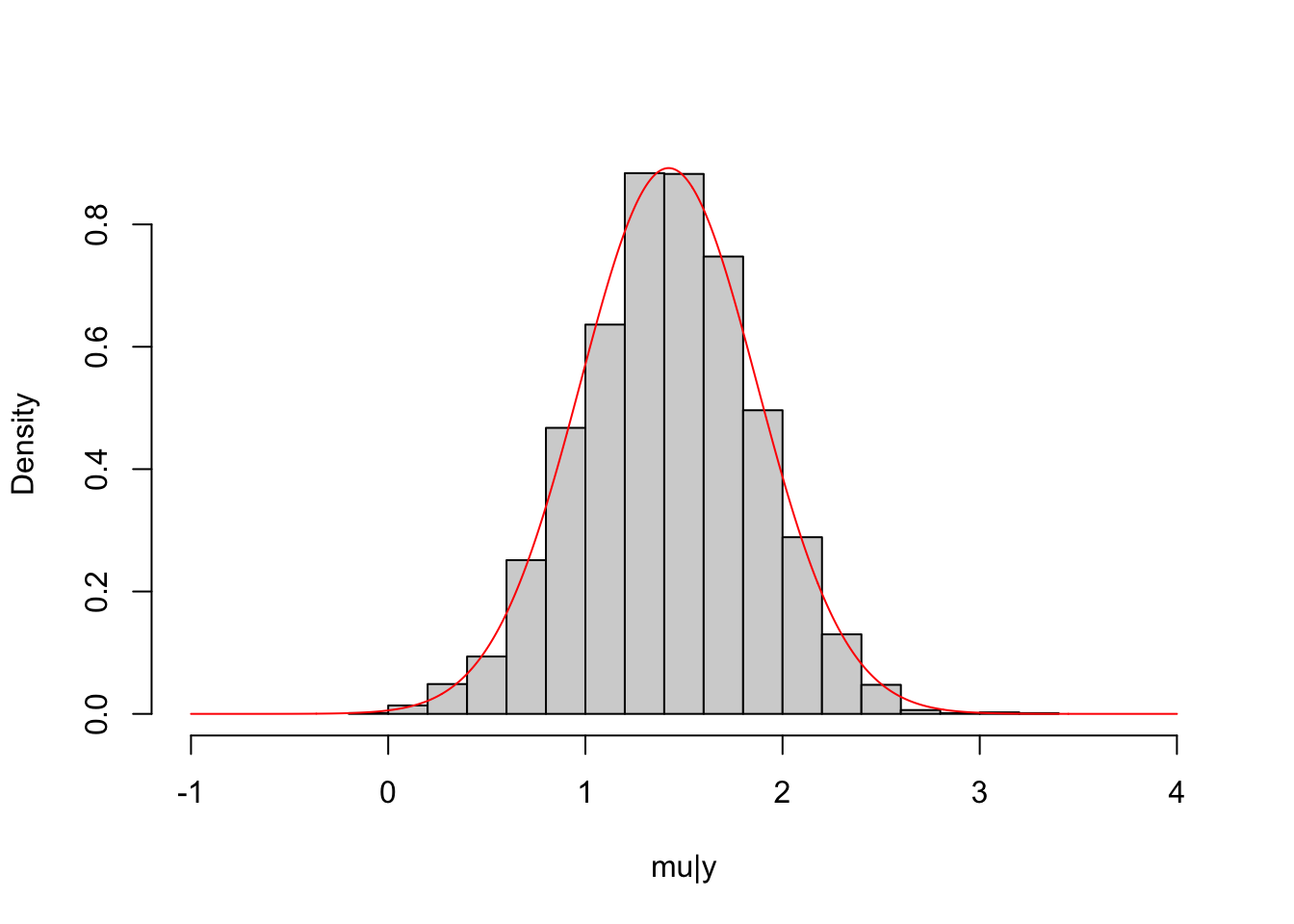
Example 3, Dirichlet-multinomial
This is the multivariate-extension of beta-binomial model.
\[ (\theta_1,\theta_2,...,\theta_K)\sim \text{Dir}(\alpha_1,\alpha_2,...,\alpha_K),\ \text{where} \sum_k \theta_k=1\ \text{and}\ \theta_k\geq 0\ \forall k \]
\[ (Y_1,Y_2,...,Y_K)\sim \text{Multinomial}(n,\boldsymbol {\theta}),\ \text{where} \sum_i Y_i=n \]
\[ p(\boldsymbol{\theta}|\boldsymbol{y})\propto \Pi_k \theta_k^{y_k}\Pi_k \theta_k^{\alpha_k-1} \]
Therefore,
\[ \boldsymbol{\theta}|\boldsymbol{y}\sim \text{Dir}(\alpha_1',\alpha_2',...,\alpha_K'), \text{where}\ \alpha_k'=\alpha_k+y_k\ \forall k \]
It can be shown that the marginal distribution of a Dirichlet distribution is a beta distribution, for example, \(\theta_1|\boldsymbol {y}\sim \text{Beta}(\alpha_1',\sum_k\alpha_k'-\alpha_1')\).
Here, we consider \(5\) categories and a uniform prior with \(\alpha_k=1\ \forall k\).
Code
# set prior and generate data
Alpha = c(alpha1 = 1, alpha2 = 1, alpha3 = 1,
alpha4 = 1, alpha5 = 1)
Theta = c(theta1 = 0.25, theta2 = 0.15, theta3 = 0.05,
theta4 = 0.35, theta5 = 0.20)
set.seed(0808)
y_multinomial = as.vector(rmultinom(1, n, prob = Theta))Code
data { // Y is the observation vector with K categories
int<lower=3> K;
array[K] int Y;
}
parameters { // Thetas are bounded and sum to 1
simplex[K] Theta;
}
model {
Theta ~ dirichlet(rep_vector(1, K));
Y ~ multinomial(Theta);
}Code
# MCMC and plot
dat_multinomial = list(K=5, Y=y_multinomial)
dirichlet_multinomial_fit = sampling(dirichlet_multinomial_model,
data = dat_multinomial)
##
Theta1_post = unlist(extract(dirichlet_multinomial_fit, pars="Theta[1]",
permuted = T))
hist(Theta1_post, freq = F, main = NULL, xlim = c(0,1),
xlab = "theta[1]|y")
lines(seq(0, 1, length.out = 1000), dbeta(seq(0, 1, length.out = 1000),
shape1 = Alpha["alpha1"]+y_multinomial[1],
shape2 = sum(Alpha[-1]+y_multinomial[-1])),
col="red")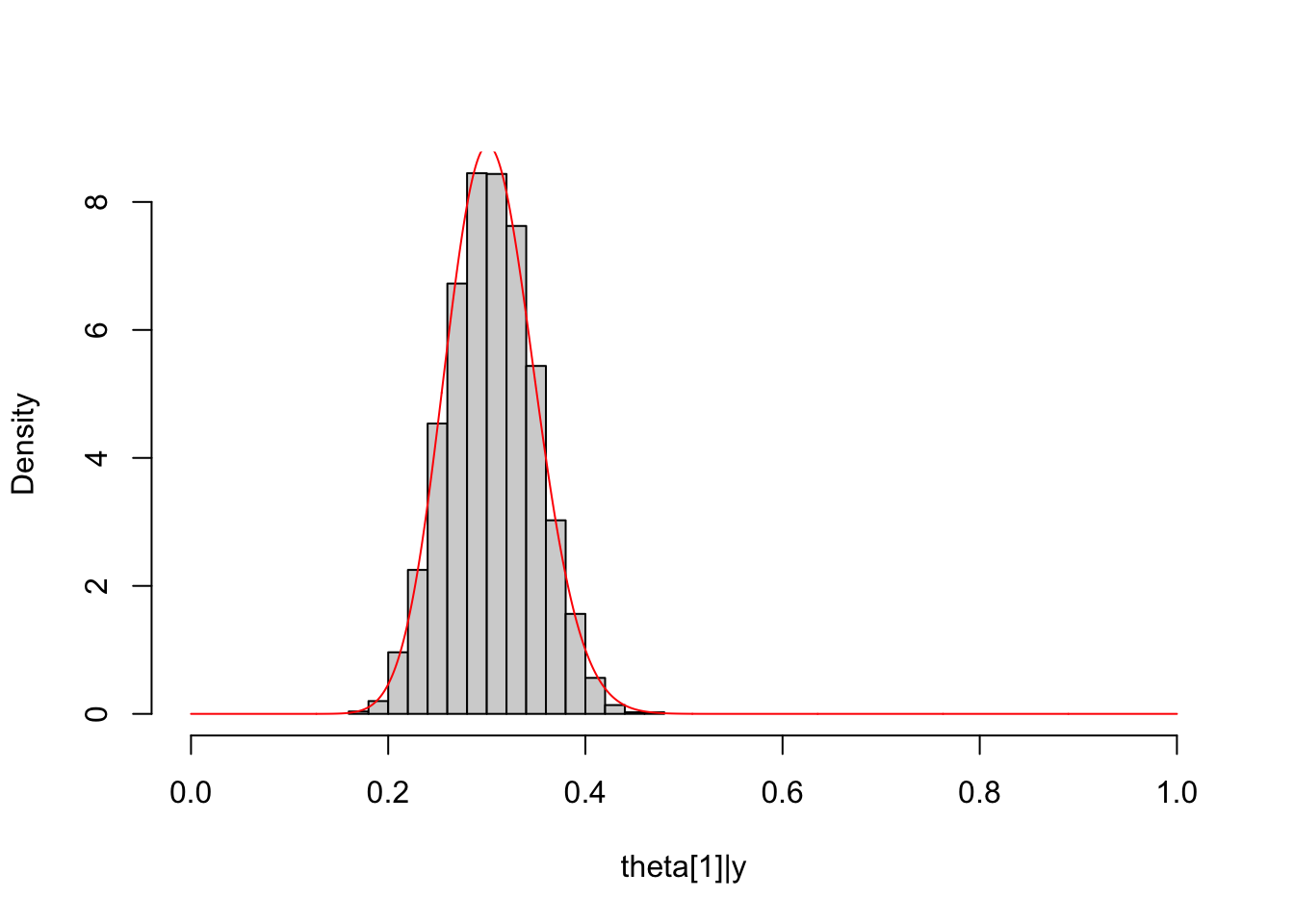
Code
##
Theta2_post = unlist(extract(dirichlet_multinomial_fit, pars="Theta[2]",
permuted = T))
hist(Theta2_post, freq = F, main = NULL, xlim = c(0,1),
xlab = "theta[2]|y")
lines(seq(0, 1, length.out = 1000), dbeta(seq(0, 1, length.out = 1000),
shape1 = Alpha["alpha2"]+y_multinomial[2],
shape2 = sum(Alpha[-2]+y_multinomial[-2])),
col="red")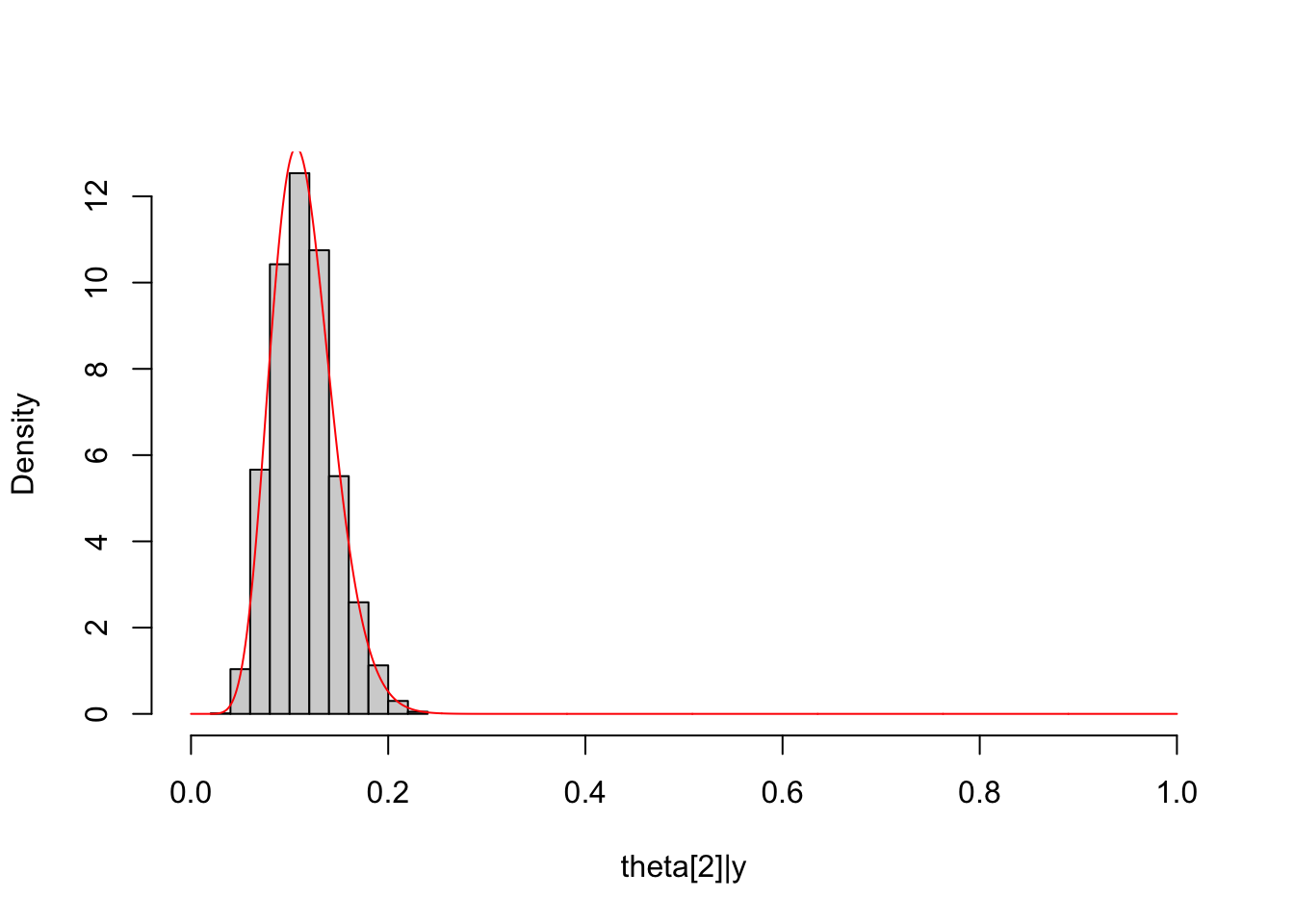
Code
##
Theta3_post = unlist(extract(dirichlet_multinomial_fit, pars="Theta[3]",
permuted = T))
hist(Theta3_post, freq = F, main = NULL, xlim = c(0,1),
xlab = "theta[3]|y")
lines(seq(0, 1, length.out = 1000), dbeta(seq(0, 1, length.out = 1000),
shape1 = Alpha["alpha3"]+y_multinomial[3],
shape2 = sum(Alpha[-3]+y_multinomial[-3])),
col="red")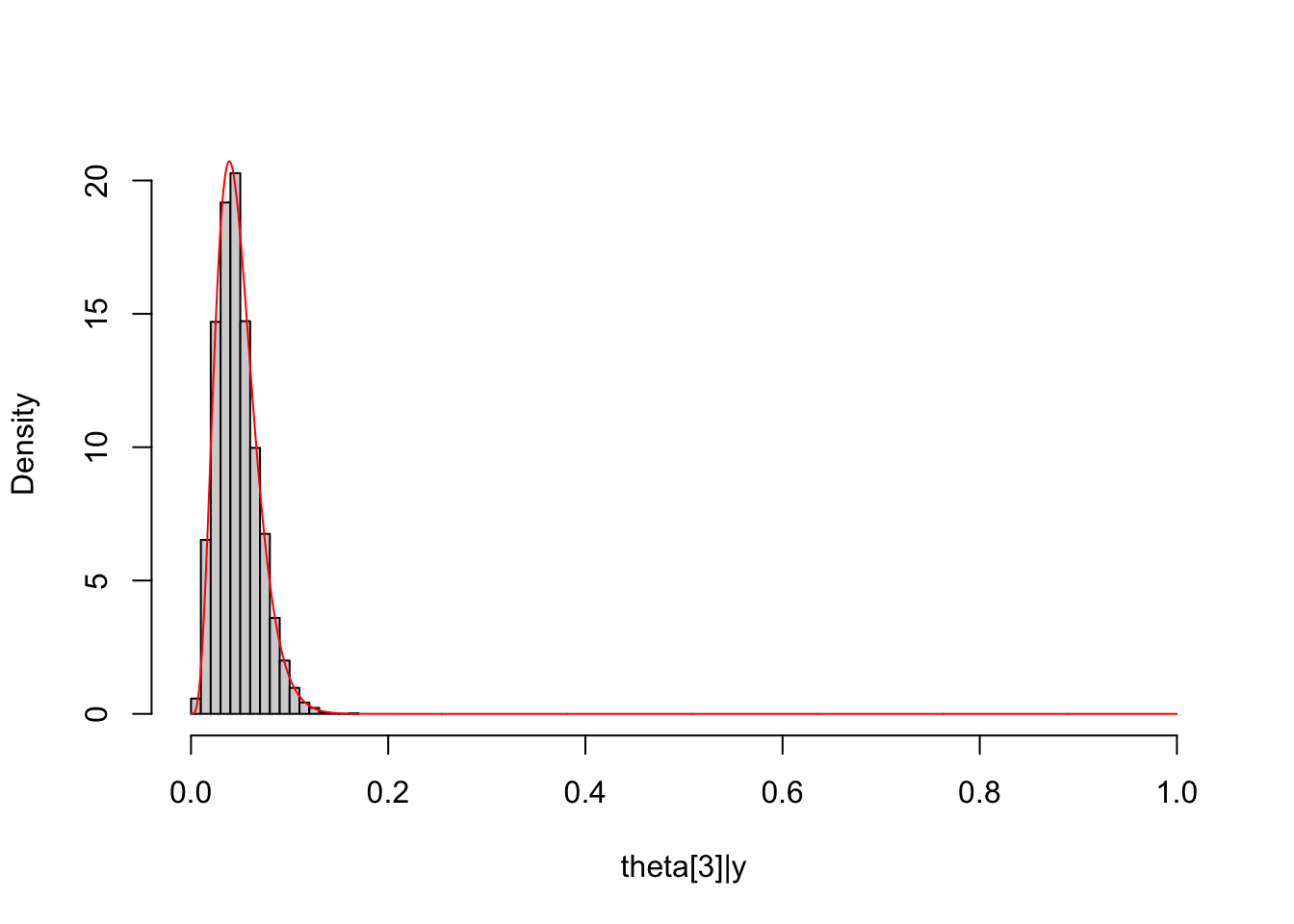
Code
##
Theta4_post = unlist(extract(dirichlet_multinomial_fit, pars="Theta[4]",
permuted = T))
hist(Theta4_post, freq = F, main = NULL, xlim = c(0,1),
xlab = "theta[4]|y")
lines(seq(0, 1, length.out = 1000), dbeta(seq(0, 1, length.out = 1000),
shape1 = Alpha["alpha4"]+y_multinomial[4],
shape2 = sum(Alpha[-4]+y_multinomial[-4])),
col="red")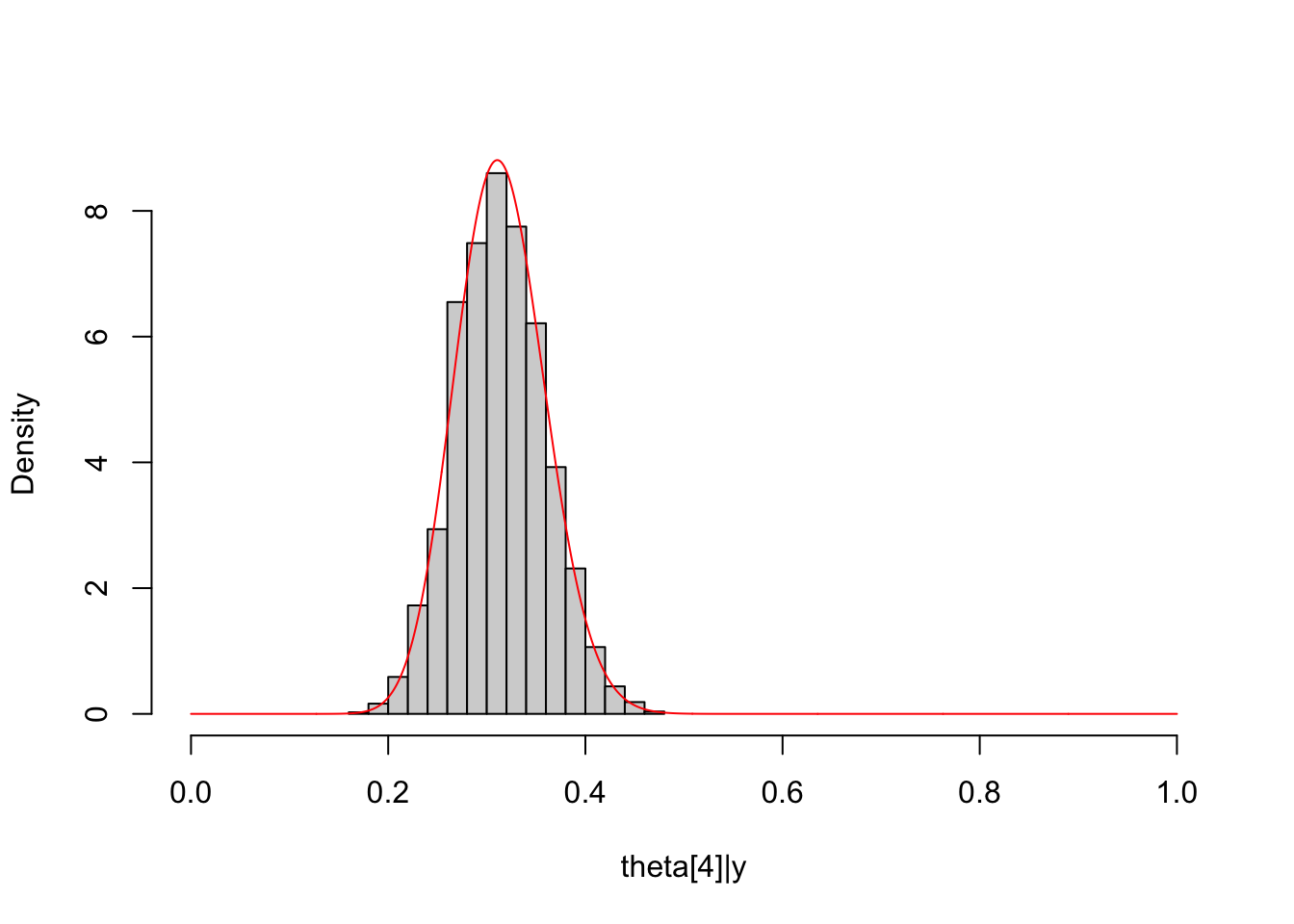
Example 4, Bayesian linear regression
Refer to the Bayesian analysis of classical regression in Chapter 14 of Bayesian Data Analysis, 3rd.
\[ p(\boldsymbol{\beta},\sigma^2|X)\propto \sigma^{-2} \]
\[ Y|\boldsymbol{\beta},\sigma^2,X\sim N(X\boldsymbol{\beta},\sigma^2I),\ \text{where}\ Y\ \text{is random vector of length n} \]
\[ p(\boldsymbol{\beta},\sigma^2|\boldsymbol{y},X)\propto \sigma^{-n}\exp(-\frac{1}{2}(\boldsymbol{y}-X\boldsymbol{\beta})^T(\sigma^2I)^{-1}(\boldsymbol{y}-X\boldsymbol{\beta}))\sigma^{-2}\\ \propto \sigma^{-(n+2)}\exp(-\frac{1}{2\sigma^2}(\boldsymbol{y}-X\boldsymbol{\beta})^T(\boldsymbol{y}-X\boldsymbol{\beta})) \]
With some algebra,
\[ \exp((\boldsymbol{y}-X\boldsymbol{\beta})^T(\boldsymbol{y}-X\boldsymbol{\beta}))\propto \exp(\boldsymbol{\beta}^TX^TX\boldsymbol{\beta}-2\boldsymbol{\beta}^TX^Ty)\\ \propto \exp((\boldsymbol{\beta}-(X^TX)^{-1}X^Ty)^T(X^TX)(\boldsymbol{\beta}-(X^TX)^{-1}X^Ty)) \]
\[ \boldsymbol{\beta}|\sigma^2,\boldsymbol{y},X \sim N((X^TX)^{-1}X^Ty, \sigma^2(X^TX)^{-1}) \]
\[ p(\boldsymbol{\beta},\sigma^2|\boldsymbol{y},X)=p(\boldsymbol{\beta}|\sigma^2,\boldsymbol{y},X)p(\sigma^2|\boldsymbol{y},X) \]
Therefore,
\[ p(\sigma^2|\boldsymbol{y},X)=\frac{ p(\boldsymbol{\beta},\sigma^2|\boldsymbol{y},X)}{p(\boldsymbol{\beta}|\sigma^2,\boldsymbol{y},X)}\\ \propto \frac{\sigma^{-(n+2)}\exp(-\frac{1}{2\sigma^2}(\boldsymbol{y}-X\boldsymbol{\beta})^T(\boldsymbol{y}-X\boldsymbol{\beta}))}{\sigma^{-p}\exp(-\frac{1}{2\sigma^2}(\boldsymbol{\beta}-(X^TX)^{-1}X^Ty)^T(X^TX)(\boldsymbol{\beta}-(X^TX)^{-1}X^Ty)}\\ \propto \sigma^{-(n+2-p)}\exp(-\frac{1}{2\sigma^2}(\boldsymbol{y}^T\boldsymbol{y}-(X^T\boldsymbol{y})^T(X^TX)^{-1}X^T\boldsymbol{y})) \]
Refer to the pdf of scaled inverse-chi-square distribution,
\[ p(\sigma^2|\boldsymbol{y},X)\propto \frac{1}{(\sigma^2)^{\frac{n-p}{2}+1}}\exp(-\frac{(n-p)\frac{1}{n-p}(\boldsymbol{y}-X\hat{\boldsymbol{\beta}})^T(\boldsymbol{y}-X\hat{\boldsymbol{\beta}})}{2(\sigma^2)}) \]
Hence,
\[ \sigma^2|\boldsymbol{y},X\sim \text{scaled Inv-}\chi^2(n-p,\frac{1}{n-p}(\boldsymbol{y}-X\hat{\boldsymbol{\beta}})^T(\boldsymbol{y}-X\hat{\boldsymbol{\beta}})) \]
\(p\) is the number of columns of the design matrix \(X\) including a column of \(1\). Recall that in frequentist classical linear regression, \(\hat{\boldsymbol{\beta}}=(X^TX)^{-1}X^T\boldsymbol{y},\ \text{Var}(\hat{\boldsymbol{\beta}})=\sigma^2(X^TX)^{-1},\ \hat{\sigma^2}= \frac{1}{n-p}(\boldsymbol{y}-X\hat{\boldsymbol{\beta}})^T(\boldsymbol{y}-X\hat{\boldsymbol{\beta}})\).
For simplification, consider \(p=2\).
Code
# generate data
set.seed(0809)
x = rbinom(n, 1, prob = 0.55) # covariate is binary
beta_0 = 0.5 # intercept
beta_1 = 0.2 # effect
set.seed(0809)
y_linear_regression = beta_0 + x*beta_1 + rnorm(n, 0, 1)
dat_linear = list(N=n, Y=y_linear_regression, x0=rep(1, n), x1=x)Code
functions {
real logposterior(real y, real beta0, real beta1, real x0, real x1, real sigma2){
return -(y-beta0*x0-beta1*x1)^2/(2*sigma2) - log(sigma2)/2;
}
}
data { // Y is the outcome vector with N observations
int<lower=0> N;
array[N] real Y;
array[N] real x0;
array[N] real x1;
}
parameters { // beta and sigma2
real beta0;
real beta1;
real<lower=0> sigma2;
}
model {
target += -log(sigma2);
for(n in 1:N){
target += logposterior(Y[n], beta0, beta1, x0[n], x1[n], sigma2);
}
}Code
bayesian_linear_fit = sampling(bayesian_linear_regression,
data=dat_linear)
beta0_post = extract(bayesian_linear_fit, par="beta0", permuted=T)$beta0
beta1_post = extract(bayesian_linear_fit, par="beta1", permuted=T)$beta1
sigma2_post = extract(bayesian_linear_fit, par="sigma2", permuted=T)$sigma2
mean(beta0_post)[1] 0.4000068Code
mean(beta1_post)[1] 0.1179789Code
mean(sigma2_post)[1] 1.217507Code
lm_fit = lm(y~x1, data = data.frame(y=dat_linear$Y, x1=dat_linear$x1))
coefficients(lm_fit)(Intercept) x1
0.4010346 0.1171188 Code
sum(lm_fit$residuals^2)/lm_fit$df.residual[1] 1.191846Code
# sigma2
scaled_inv_chi2_pdf = function(x, nu, tau2){
return((((tau2*nu/2)^(nu/2))/(gamma(nu/2)))*(exp(-nu*tau2/(2*x))/(x^(1+nu/2))))
}
hist(sigma2_post, freq = F, main = NULL, xlim = c(0.5,2.5),
xlab = "sigma2|y")
lines(seq(0.5, 2.5, length.out = 1000), scaled_inv_chi2_pdf(seq(0.5, 2.5, length.out = 1000), nu = lm_fit$df.residual, tau2 = sum(lm_fit$residuals^2)/lm_fit$df.residual),
col="red")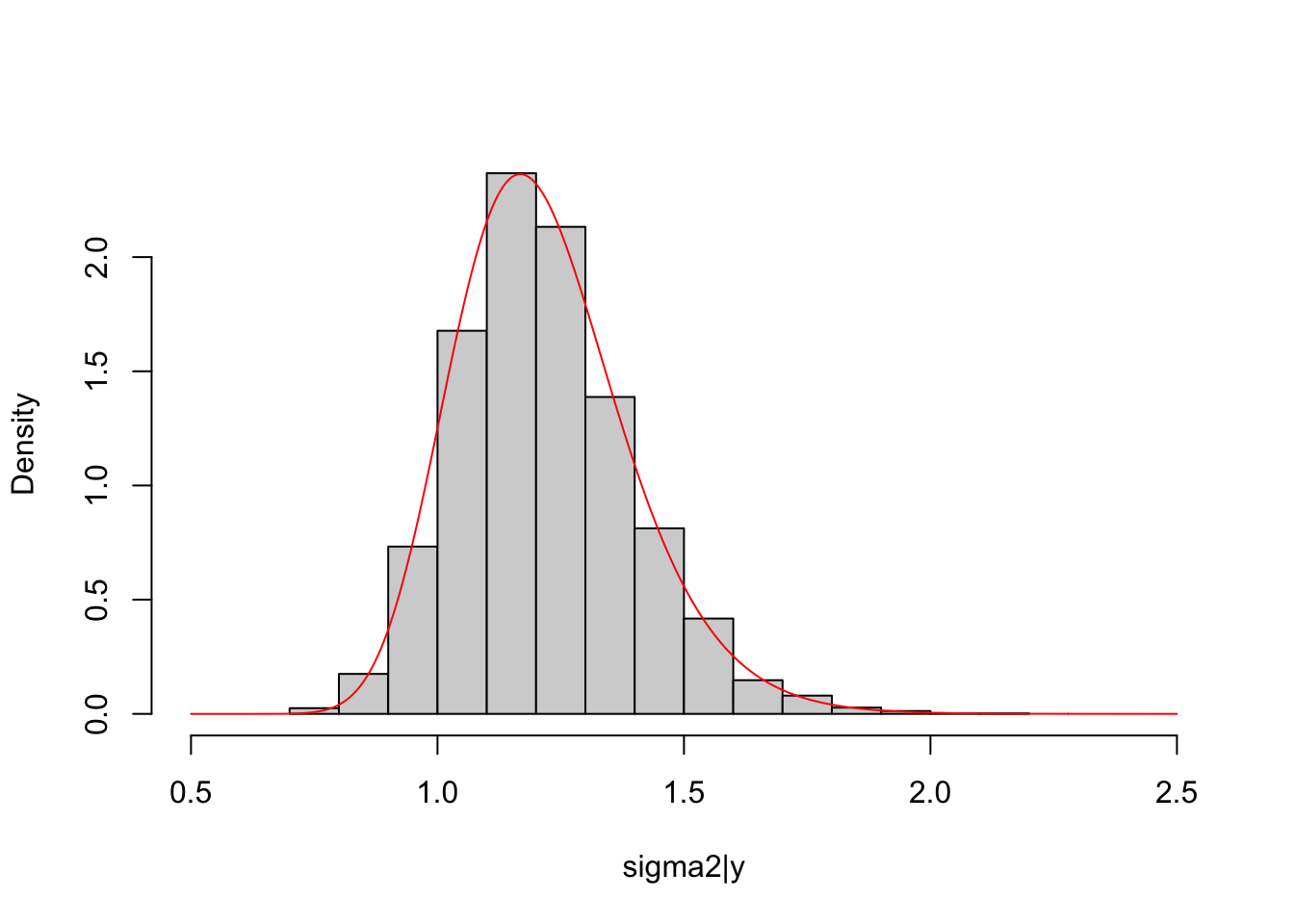
Code
# beta
library(MASS)
X = matrix(c(dat_linear$x0, dat_linear$x1), ncol = 2, byrow = F)
Beta = sapply(sigma2_post, function(z) mvrnorm(n=1, mu = solve(t(X)%*%X)%*%t(X)%*%as.matrix(dat_linear$Y, ncol=1), Sigma = z*solve(t(X)%*%X)))
## beta0
hist(beta0_post, freq = F, main = NULL, xlim = c(-0.5,1.5),
xlab = "beta0|y")
lines(density(Beta[1, ])$x, density(Beta[1, ])$y,
col="red")
Code
## beta1
hist(beta1_post, freq = F, main = NULL, xlim = c(-1,1.5),
xlab = "beta1|y")
lines(density(Beta[2, ])$x, density(Beta[2, ])$y,
col="red")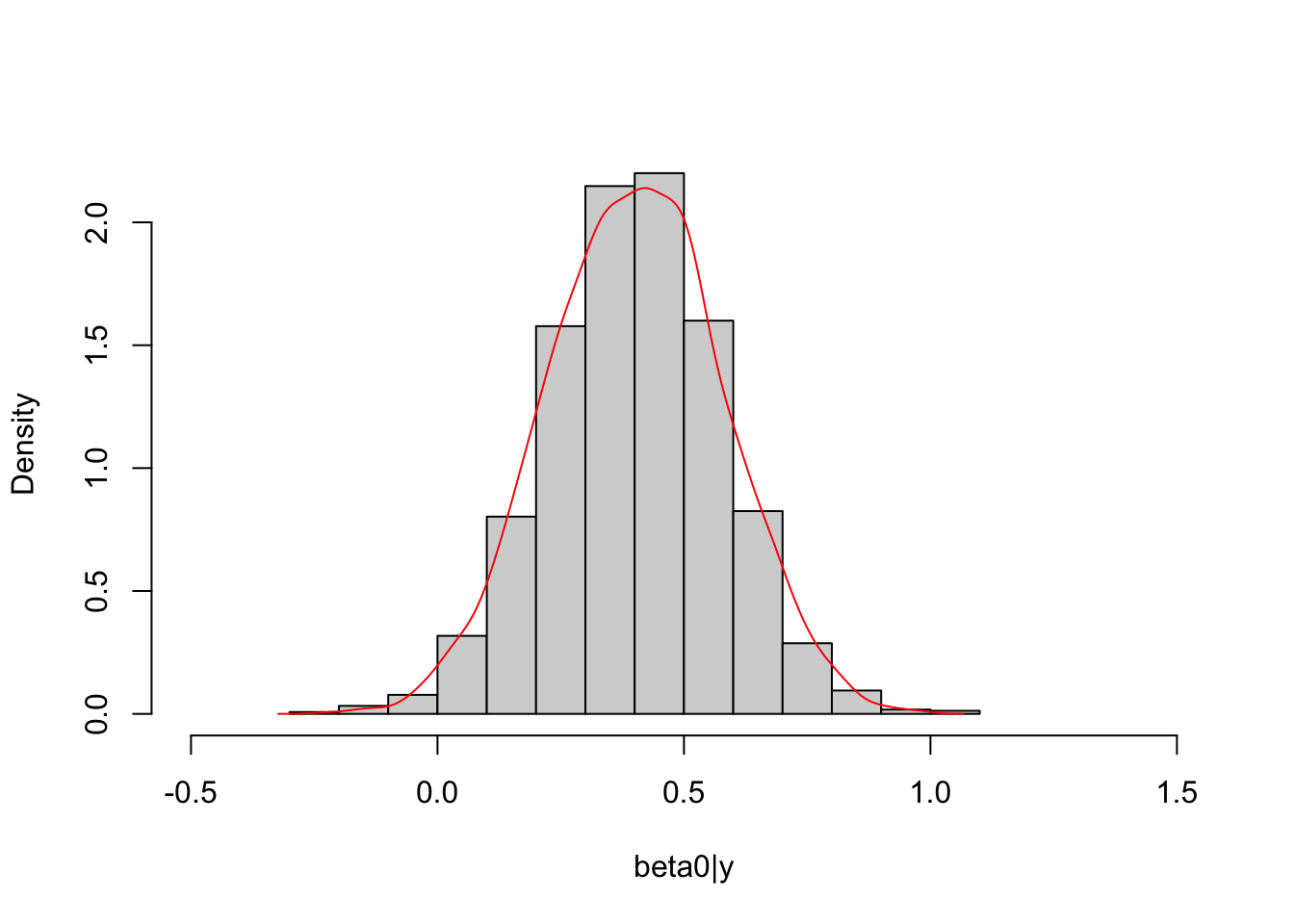
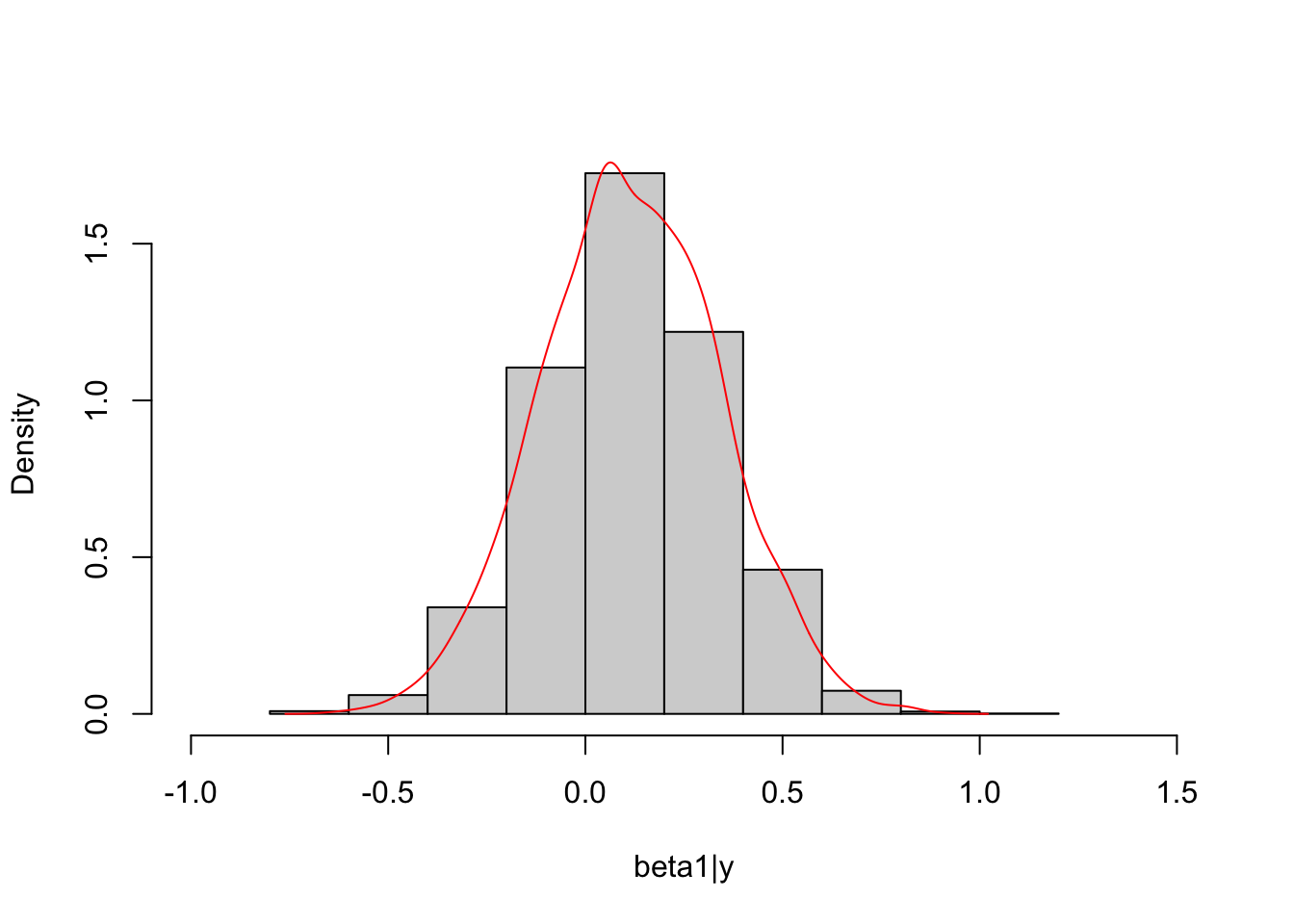
The marginal posterior distribution of \(\boldsymbol \beta\) is unknown up to this point and its conditional posterior distribution is known, multivariate normal. Thus, we can simulate posterior draws of \(\boldsymbol \beta\) based on the conditional distribution and simulated draws of \(\sigma^2\) to compare with draws obtained from Stan.